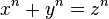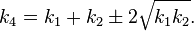Today I talked to one of my Pagalguy friend. He was right in saying that my blog is not good for all. I agree. What I try to discuss, here, is obviously not for all and sometimes the concept becomes too tough to understand. And there are a lot of people who are unable to attend coaching classes due to different reasons. So being a pagalguy member I should help them. And if this section can help you a little, I will consider myself blessed. There will be two sections CAT CLASSIC and CAT SHOT, which will only concentrate on cracking CAT. Though this is, once I have written in my another blog
The Unfinished Evening
Here it goes.
Introduction
In ancient Babylon, a sexagesimal(base 60) was in use.In India a decimal system was in place during Harappan period.
It is generally acknowledged that concept of zero,crucial to development of science,is India’s contribution to the world, which was given to Europe through the Arabs.The ancient India astronomer Brahmagupta is credited with having put forth the concept of zero first time.
Another famous Indian mathematician developed the concept of pi as 3.1416(circa 500 AD) claiming,for the first time it was an approximation.Pi represents the number reflecting how many times a circle’s diameter may be divided into its circumference
In the following problem we may get confused:
1+a+a^2+….n terms = (a^n-1)/(a-1) ; if a=1 then 0/0=n, so where lies the pitfall?
No man! It’s correct. 0/0 takes any given value for different n. So it is undefined.We can say something either exists, or it doesn’t. If it exists, then it has a quality that we call number associated with it, and if it doesn’t exist we call this absence, zero.
145 = 1! + 4! + 5! only number which can be expressed as the factorial summation of it’s individual digit.
————————————————————————————————————————————————————Number theory is playing a pivotal role so far as management entrance examinations like CAT/XAT/JMET/IIFT/MAT are concerned. So it’s imperative that good grasp on this topic is essential to ace quantitative section. The whole chapter is divided into three topics.
Topic 1: Numbers and Divisibility
Divisibility Fundamentals
(i)Any composite number
N=a^m * b^n * c^p [a,b,c all are prime numbers] has number of factors equals to
(m+1)*(n+1)*(p+1)
(ii)sum of it’s divisors is given by
(a^m+1 – 1)/(a-1)*(b^n+1 – 1)/(b-1)*(c^p+1 – 1)/(c-1)
(iii)Product of it’s divisors equals to
N^[(m+1)*(n+1)*(p+1)/2]
(iv)The number of ways in which the number can be resolved into two factors are
(m+1)*(n+1)*(p+1)/2 and if the number is a square number then number of ways would be
[(m+1)*(n+1)*(p+1)+1]/2
Condition for two divisors of any number n to be co-prime to each other
(i)Let N=a^m*b^n has
(m+1)(n+1)-1+mn numbers of factors which are co-prime to each other. If N=12, then as 12=2^2*3,so it has (2+1)*(1+1)-1+2=7 sets which are co-prime to each other.They are: (1,2),(1,3),(1,4),(1,6),(1,12),(2,3),(3,4).
(ii)Similarly we can deduce the formula for higher orders.If N=a^m*b^n*c^p then it will have
(m+1)(n+1)(p+1)-1+mn+np+mp+3mnp co prime factors.Actually it is a deduction of previous formula.As N=a^m*b^n has (m+1)(n+1) -1+mn number of factors So N=d^[(m+1)(n+1)-1+mn]*c^p has[(m+1)(n+1)+mn-1+1](p+1) -1+[(m+1)(n+1)-1+mn]p number of factors which is equal to (m+1)(n+1)(p+1)-1+mn+np+mp+3mnp.
The number of ways to express a number by means of product of two co-prime numbers
2^(n-1) ways; where ‘n’ represents number of prime factors of that number. Let N=12=2^2 x 3.Therefore it can be expressed as 2^(2-1)=2 ways as the product of two co-prime numbers.They are (1,12) and (3,4).
Euler’s Function and it’s application
Euler function is related to prime numbers counting theorem.By using this we can count number of co-primes less than of a number.It is denoted by φ(N). φ(N) is known as Euler’s function of number N. N=a^m*b^n*c^p then
φ(N) = N(1 – 1/a)(1 – 1/b)(1 – 1/c) and so on for any higher terms.[N.B.:a,b,c all are prime numbers] Let, we have to count all numbers which are co-prime to 12 and less than 12.Therefore we have to count φ(12).As 12=2^2*3, So φ(12)=12(1 – 1/2)(1 – 1/3)=12*(1/2)*(2/3)=4 and obviously pairs are (1,12),(5,12),(7,12),(11,12) or in simple terms 1,5,7,11 are those numbers which are less than 12 and co-prime to 12.
Dirichlet’s theorem
If a is positive and hcf(a,b)=1,then there are infinitely prime numbers in the form of an+b.
Elucid’s Theorem
If p is a prime number and it divides ab(product of two integers a&b) then either p divides a or p divides b.This proposition is known by Elucidian’s lemma.
Prime Number
Till now, all attempts made to arrive at a single formula to represent all prime numbers proved to be fruitless.The main reason behind of it is all because there is no symmetricity between the differences among them.One standard notation for prime number is N^2+N+41 where -39=<39.Some properties of prime number are elucidated here.
(i)All prime numbers end in 1,3,7 or 9.(except 2,5).
(ii)Fermat’s little theorem
if p is prime then a^p leaves a remainder a when divided by p or in other words a^p-a=0(mod p)
(iii)Wilson’s theorem
an integer p will be prime only when (p-1)!+1 is divisible by p.
(iv)Bertrand’s Postulate says, if n is a positive integer greater than 1, then there is always a prime number p n
<2n.
(v)All prime numbers greater than 3 can be expressed as 6K+1 or 6K-1. But converse is not true always.eg.:13(6*2+1) is prime but 25(6*4+1) is not prime.
(vi)1/p (p is prime other than 2 &5 ) always a recurring decimal of period (p-1).It is true for other bases q, provided p is not a prime factor of q.
Perfect Number
Perfect number is defined as a positive integer which is the sum of its proper positive divisors, that is, the sum of the positive divisors excluding the number itself.First four perfect numbers can be generated by 2
n−1(2
n − 1).[Where 2
n − 1 is a prime number].This are all even perfect numbers.All even perfect numbers (except 6) digital root 1.
Armstrong Number
Armstrong numbers are the sum of their own digits to the power of the number of digits. example:153 = 1³ + 5³ + 3³[as sum of the digits are 3], 1
4 + 6
4 + 3
4 + 4
4 = 1634.
Rare Number
The numbers, which gives a perfect square on adding as well as subtracting its reverse are rare and hence termed as Rare Numbers.If R is a positive integer and R1 is the integer obtained from r by writing its decimal digits in reverse order, then R + R1 and R – R1 both are perfect square then R is termed as Rare Number. For example: R=65, R1=56 we can write R+R1 = 65+56 = 121 = 112 & R-R1 = 65 – 56 = 9 = 32.So 65 is a Rare Number.
Properties of co-prime numbers
(i)The numbers
a and
b are coprime if and only if there exist integers
x and
y such that
ax +
by = 1.
(ii)If
a and
b are coprime and
bx =
by (mod
a), then
x =
y (mod
a).
(iii)Two natural numbers
a and
b are coprime if and only if the numbers 2
a-1 and 2
b-1 are coprime.
Fermat’s last theorem
If x, y, z and n are integers, there are no solutions of x^n+y^n=z^n with n>2 and x,y,z>0.
Topic 2:Cyclicity, Factorial and Modulo Arithmetic
Cyclicity :
The last digit of the exponents of all nubers have a cyclicity.That is,every Nth power of the base shall have the same digit.Now we can consider the following table to reveal the pattern.
Consider exponents of 2. 2^1=2|2^2=4|2^3=8|2^4=16|2^5=32|2^6=64.So the same unit digit 2 comes again when the exponent is increased by 4.Same pattern is followed for other exponents also.So cyclicity or period of 2 is 4.
Similarly we can conclude: 0,1 5,6 have cyclicity 1, 2,3,7,8 have cyclicity 4,4,9 have cyclicity 2.
We can take an easy example to illustrate it.
Problem:
Find the unit digit of 7^23 x 4^21
7^23=7^(4*5+3)=7^4*5 x 7^3=(..1) x (343)=…3[As 7 has cyclicity 4, so 7^4n always yields unit digit 1.] Similarly 4^21=4^(2*10+1)=4^(2*10)*4=..1*4=..4[As 4 has cyclicity 2, so 4^2n always produces unit digit 1.] 7^23*4^21=(..3)x(..4)=…2. Required unit digit is 2.
How to find last two digits of a number
(x+a)^n= x^n+ nc1*x^n-1*y+nc2*x^n-2*y^2+….+y^n. By application of binomial expansion we can do any problem under this category. We can do this kind of problem by using modular arithmetic or by pattern method too.Barring all of these there is also another process to solve.I hope that procedure will help us to solve any problem in lesser time.So I think it would be better to discuss them in another page.
Factorial
Factorial is another important part of Number System.Generally question comes from either pattern recognition or from determining highest power diving a factorial number.
Thus approach to finding highest power of p(p is prime) in y! is [y/x]+[y/x^2]+[y/x^3]+…….where [] represents greater integer function or gint function.Which determines just integral part of [].It can be used to determine number of zeros in a factorial number.
P.S.:1!+2!+3!+4!+5!=1+2+6+24+120=153 so 1!+2!+3!+4!+…..+n! always yields unit digit 3 and it does not depend on n.Where n can be infinitely any.As 5! is the first number which gives unit digit 0. 10! is the first number which has last two digits 0 and so on & so forth.
Modulo Arithmetic And Remainder Theorems
Suppose n divides a and gives a remainder b then it can be expressed in the format of modulo arithmatic. a=b(mod n). Modular arithmetic follows addition, subtraction and multiplication rule.
If a1=b1(mod n) and a2=b2( mod n) then; (i)(a1+a2)=(b1+b2)(mod n) (ii)(a1-a2)=(b1-b2)(mod n),(iii)(a1.a2)=(b1.b2)(mod n).
Euler’s Remainder Theorem:
We alrealdy know what is Euler’s function.Now according to this theorem a^ φ(N)=1(mod N) where a and N are co prime to each other.φ(N) is also known as ORDER of a modulo N.
Corollary:
(a) 1/a=a^ [φ(N)-2](mod N) when a & N are co prime to each other.
(b) a and b are relatively prime positive integers,
then there exist integers m and n such that a^m + b^n = 1 (mod ab)
(ii)
Fermat’s Little Theorem:
If p is a prime number,then a^(p-1)=1(mod p)
(iii)
Chinese Remainder Theorem:
If N=a*b where a & b are co prime,M is such that M=r1(mod a) and M=r2(mod b) then M=a*r2*x+b*r1*y(mod N) where ax+by=1.
More concepts:
(1)gcd(a^m – 1,a^n – 1)=a^gcd(m,n) – 1 for all positive integers m,n & a>1.
(2)ax+by =n has an non negative integer solution if gcd(a,b)=n.
(3) 1/x+1/y=1/n is a equation where x,y,n are positive integers & n>1.Now we have to determine the number of ordered pairs of (x,y). For this at first we have to do prime factorization of n=a^p1*b^p2*c^p3*….Therefore the number of positive solution se would be (2p1+1)(2p2+1)(2p3+1)…..
(4)Divisibility by 7, 11, and 13
Let a number be ….kjihgfedcba where a, b, c, d, are respectively units digits, tens digits, hundreds digits, thousands digits and so on. Starting from right to left, we make groups of three digit numbers successively and continue till the end. It is not necessary that the leftmost group has three digits.
Grouping of the above number in groups of three, from right to left, is done in the following manner 0kj,ihg,fed,cba. Groups are denoted as (4,3,2,1).
We add the alternate groups (1
st , 3
rd , 5
th etc.. and 2
nd , 4
th , 6
th , etc..) to obtain two sets of numbers, N
1 and N
2 .
In the above example, N
1 = cba + ihg and N
2 = fed + kj
Let D be difference of two numbers, N
1 and N
2 i.e. D = N
1 – N
2 .
If D is divisible by 7, then the original number is divisible by 7.
If D is divisible by 11, then the original number is divisible by 11
If D is divisible by 13 then the original number is divisible by 13.
Corollary:
Any six-digit, or twelve-digit, or eighteen-digit, or any such number with number of digits equal to multiple of 6, is divisible by EACH of 7, 11 and 13 if all of its digits are same .
For example 666666, 888888888888 etc. are all divisible by 7, 11, and 13.
(5)Divisibility by 9
Sum up all digits of a number, divide it by 9.The remainder is equal to the remainder when the original number is divided by 9.
Properties of squares
(1)Any square number can be expressed as 3k or 3k+1.
(2)Square of an odd number can be expressed as 4k+1,square of an even number can be expressed as 4k.
(3)Last digit of a square number cannot be 2,3,7,8.
(4)Square of any prime number can be expressed as 6K+1(p>3)
(5)If last digit of a number is odd the previous number would be even.
(6)A square number cannot be a perfect number.
Seed Number or Digital Root
If we sum up all the digits of a number till then single digit is arrived, then that single digit would be the seed of that number
Properties:
(i)To determine a seed we have to divide the number by 9.The remainder obtained will be the seed. If the number becomes perfectly divisible 9 then seed number would be 9.
(ii)A perfect square cannot have any seed number among 2,3,5,6,8.
(iii)6! onwards all number has equal seed number 9.
(iv)The difference between one number and it’s sum of the digits is always divisible by 9.
e.g.:For 68 it’s sum of digit is 15. So difference is 68-14=54.Divisible by 9.
Hope these concepts would help us to open the knot of problems