1,2,5,14,42,?
You may face trouble in finding though. But here is the formula
Tn=1/(n+1)*2nCn=(2n)!/[(n+1)!*n!] [For n>=1]
So T5=132.
The number of this series is popularly known as CATLAN numbers. And in different counting problems. I will try to explore some of them.
(A)Mountain Ranges and Diagonal Avoiding Paths
(i)How many mountain ranges you can draw using n upstrokes(/) and n downstrokes{\)
Drawing the above phenomenon would reduce our burden.
n=1: /\ =>1 way
n=2: /\/\, /\ => 2 ways
/ \ /\
n=3: /\ /\ /\, /\ /\ /\/\ / \ => 5 ways
/ \/\, /\/ \, / \, / \
Going like this it will generate nothing but the series of CATLAN numbers. For n=4 obviously we will get 14 distinct mountain ranges and so on.
(ii)Diagonal Avoiding Paths
In a grid of n×n squares, how many paths are there of length 2n that lead from the upper right corner
to the lower left corner that do not cross the diagonal dotted line from upper right to lower left? In
other words, how many paths stay on or above the main diagonal.
Again answer is noting but 4'th CATLAN numbers of the series. i.e. 14. And look it's not different than the arrangement of mountain ranges. [Follow the arrowhead paths]
(B)Triangulation of a convex polygon
For a convex ploygon having n sides (n>=4) total number of triangulation will be T(n-2) th term of the CATLAN series.
For n=6 obviously we will get 14 triangulations.
(C)Handshaking Lemma
If, 2n people are seated around a circular table, then in Tn ways they can shake their hands simultaneously such that at no instance the arms will cross each other.
Application
If 16 people are sitting in a circular table,in how many ways can all of them be simultaneously
shaking hands with another person at the table in such a way that none of the arms cross each other?Solution:
2n=16 =>n=8
Total ways T8 =16!/9!*8!=1430.
Hope you have enjoyed this concept session.

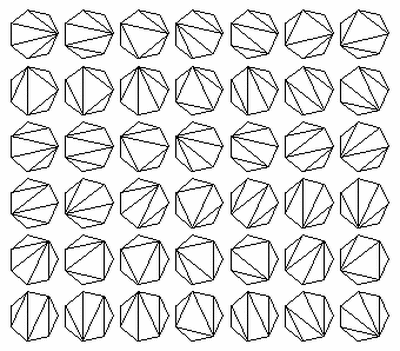
No comments:
Post a Comment